Sets

A set is a collection of objects, called elements.

Sets in mathematics, are simply a collection of distinct objects forming a group. A set can have any group of items, be it a collection of numbers, days of a week, types of vehicles, and so on. Every item in the set is called an element of the set. Curly brackets are used while writing a set. A very simple example of a set would be like this. Set $A=\{2,4,6,8,10\}$

Set notation

Sets can be finite or infinite and can be written in three ways: tabular, set builder notation or descriptive.

Tabular notation (Roster form)

In this kind of set notation, the elements of the sets are enclosed in curly brackets separated by commas. For example:
$A=\{2,4,6,8,10\}$

Semantic (Descriptive) form

In the Semantic form, all details regarding the set are given in words. For example, if we want to write a set of all the prime numbers less than 100, it will be written as:

{prime numbers less than 100} or either "A set of prime numbers less than 100".

Set builder notation

The set builder notation has a certain rule or a statement that specifically describes the common feature of all the elements of a set.

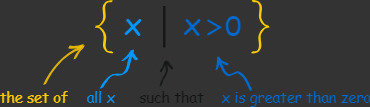
Some people use ":" instead of "|", so they write { x : x > 0 }.

If you want to include more than one condition, you write them after "|" separated by a comma or by the logical conjunction symbol $\wedge$, indicating "and".

It is also normal to show what type of number x is, like this:

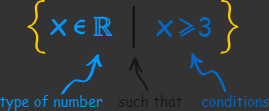
See number types.

Universal Set

The universal set. It's a set that contains everything. Well, not exactly everything. Everything that is relevant to our question.

Elements of a Set

To denote that an element is contained in a set, the symbol '∈' is used. In the set $A=\{2,4,6,8,10\}$, 2 ∈ A. If an element is not a member of a set, then it is denoted using the symbol '∉'. For example, 3 ∉ A.

Subsets

When we define a set, if we take pieces of that set, we can form what is called a subset.

To represent a subset we use the symbol $\subseteq$. Using this symbol we can express subsets as $A\subseteq B$. To represent that A is not a subset of B, it would be as $A⊈B$.

Example: the set {1, 2, 3, 4, 5}

A subset of this is {1, 2, 3}. Another subset is {3, 4} or even another is {1}, etc.

But {1, 6} is not a subset, since it has an element (6) which is not in the parent set.

Proper Subsets

Let A be a set. Is every element of A in A?
Yes. So that means that A is a subset of A. It is a subset of itself.

This doesn't seem very proper. If we want our subsets to be proper we introduce proper subsets:

Proper subsets are represented by $\subset$ and not a proper subject by $\not\subset$.

Empty set

A set with zero elements is represented either by {} or by $\varnothing$.

Empty Set and Subsets

We have a set A. We won't define it any more than that, it could be any set. Is the empty set a subset of A?

Going back to our definition of subsets, if every element in the empty set is also in A, then the empty set is a subset of A. But what if we have no elements?

It takes an introduction to logic to understand this, but this statement is one that is "vacuously" or "trivially" true.

A good way to think about it is: we can't find any elements in the empty set that aren't in A, so it must be that all elements in the empty set are in A.

So the answer to the posed question is a resounding yes.

Cardinal Number of a Set

The cardinal number, cardinality, or order of a set denotes the total number of elements in the set.
For infinite sets, all we can say is that the order is infinite.

Cartesian product

Operations

Sets operations

References

Math is fun - sets introduction
Math is fun - set builder notation
CollegeDunia - Set theory
Cuemath - Sets